INTRODUCTION
To give you an idea how to solve nonograms, we show you some steps you can use to apply when solving a nonogram with one colour. However, there are more logical steps you will need to use if you want to solve all nonograms.
Click
here for an example how to solve a nonogram with two colours.
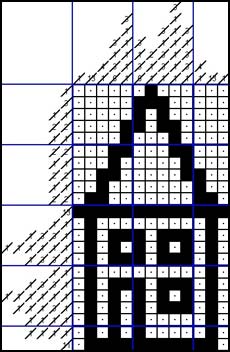
We will start with the following blank nonogram:
BASIC PRINCIPLES
A nonogram consists of rows (horizontal) and columns (vertical), whereby per row or column numbers indicate how many squares of a certain colour appear in that row or column. When a reference is made to a column number, then you need to start counting from the left most column (which is column number 1). When a reference is made to a row number, then you need to start counting from the top most row (which is row number 1).
For example: in column 2 you will find one black number (13). This means that somewhere in that column there is a range of 13 consecutive black squares.
In column 3 you will find two black numbers (4 and 1). This means that somewhere in this column there is a range of 4 consecutive black squares and below it, separated by at least one white square, you will find a ‘range’ of one black square.
In the program and in this example a dot means that it is certain that the square remains white.
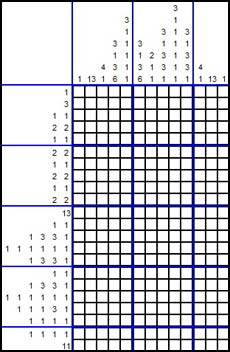
HOW TO SOLVE A NONOGRAM STEP 1
Consider row 11. It is given that there is one range of 13 consecutive black squares. Since the width of the nonogram is exactly 13 squares, this means that all squares in the row are black. To indicate that you have completed a range of squares you can put a diagonal line through the corresponding number.
The figure is as follows:
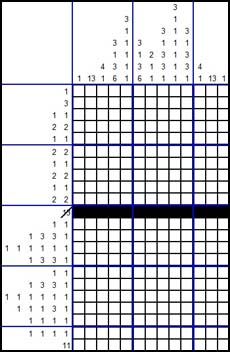
HOW TO SOLVE A NONOGRAM STEP 2
Consider row 22 (the bottom row). It is given that there is one range of 11 consecutive black squares. When we consider the possibilities, then we realise that in one extreme case the range may run from the left most square (column 1) up to column 11 and in the other extreme case it runs from column 3 up to the right most square (column 13). This implies that in all possible cases the squares in columns 3 up to 11 will have to be black. The result of this is as follows:
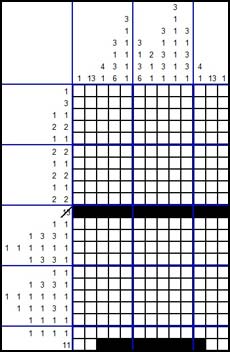
HOW TO SOLVE A NONOGRAM STEP 3
Next consider column 3. We know that the last square is black. So this is the end of the 'range' of 1 black square. Since this range is complete and the range above it is black, too, we know that the square immediately above it cannot be black, but has to be white. To indicate this we use a
dot.
A similar reasoning can be applied to column 4. The black square must be the last square of a range of 6 squares. The 5 squares above it can be made black. The square above this range of 6 has to be white.
The same we can do with the other columns (5 up to 11).
We can also cross out the corresponding numbers above the columns
The result will be as follows:
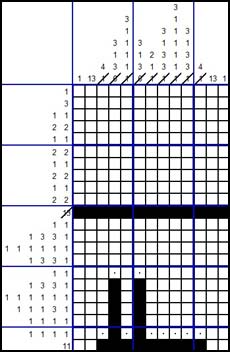
HOW TO SOLVE A NONOGRAM STEP 4
Consider the rows 18 and 20. They only contain ranges of length 1, so we know that the adjacent squares cannot be black and we use dots again to indicate this.
The same applies to the columns 1 and 13. We have found the only range of length 1 already. The remainder of both columns has to be white and therefore we can use dots to indicate this.
Finally we apply the reasoning of step 2 to columns 2 and 12.
The result is as follows:
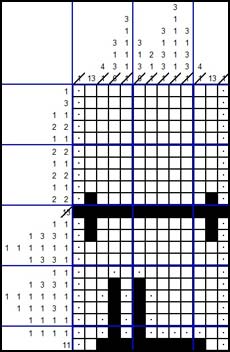
HOW TO SOLVE A NONOGRAM STEP 5
Row 12 contains two ranges of length 1, which we both have found, so we can complete the row with dots and cross out the corresponding numbers.
This gives an additional dot below the black square in column 3. The black square becomes the last square of the range of 4 squares. We can extend the range upwards. We have found all ranges in column 3, so we can fill the rest of the column with dots and cross out the corresponding numbers.
The result is as follows:
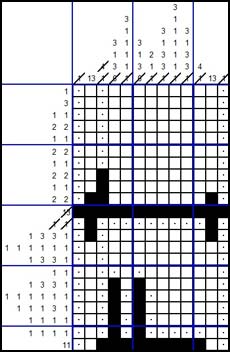
HOW TO SOLVE A NONOGRAM STEP 6
Consider row 2, which contains a range of 3 black squares. Obviously, this range does not fit between the dots in column 1 and column 3, so we can put a dot in column 2.
Because of this, the range of 13 black squares in column 2 starts at least in row 3 and runs at least up to row 15.
Note that the ranges in row 17 can be positioned in only one way!
This leads to the following result:
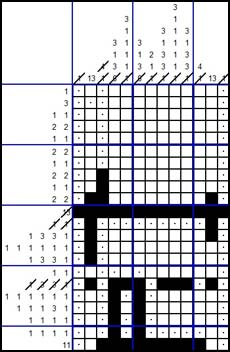
HOW TO SOLVE A NONOGRAM STEP 7
It is now clear that the black square in column 8 and row 17 belongs to a range of length 3. Therefore the square in row 20 of column 8 has to be white and we can put a dot in that square.
The result is as follows:
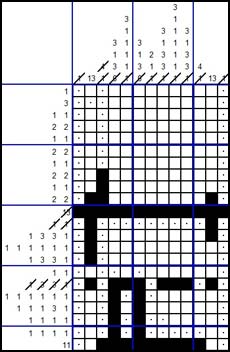
FINAL RESULT
You now have some basic logic skills to solve a nonogram and if you keep using these skills you can solve the nonogram completely!
This is what you should get: